فیلم رایگان گرادیان کاهشی چیست در هم‌رویش منتشر شد. این صفحه از هم‌رویش شامل متن مقاله + فیلم است. در این صفحه شما با مفهوم و اجرا در توابع تک متغیره تا چند متغیره آشنا می‌شوید. علاقمند به لینک زیر مراجعه کنند:
گرادیان کاهشی چیست؟ — مفهوم و اجرا در توابع تک متغیره تا چند متغیره
درباره گرادیان کاهشی چند متغیره – درک شهودی
اول از همه، بیایید یک درک شهودی از گرادیان کاهشی چند متغیره بدست بیاوریم. اعمال گرادیان کاهشی به یک تابع چند متغیره، واقعا به چه معناست؟
سعی می‌کنیم این موضوع را با تجسم موارد زیر به شما توضیح دهیم:
- تابع هدف چند متغیره
- چگونه گرادیان نزولی با این تابع کار می‌کند
به یاد بیاورید که گرادیان کاهشی، یک الگوریتم برای یافتن حداقل مقدار یک تابع است. بنابراین، هدف ما در اینجا، یافتن کمترین مقدار یک تابع است که بیش از یک متغیر داشته باشد.
در پست قبلی، از این تابع درجه دوم تک متغیره به عنوان مثال استفاده کردیم:
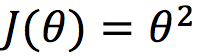
و در ادامه، با یک تابع درجه دوم دو متغیره J(θ1, θ2) به صورت زیر سروکار داریم:
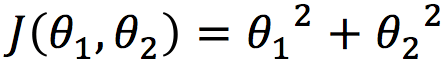
شکل 1، J(θ1, θ2) را به چند صورت مختلف به تصویر می‌کشد – نمایش سه بعدی در سمت چپ (شکل 1a) و مرکز (شکل 1b) و یک نمایش کانتوری (شکل 1c) در سمت راست.
نمودار کانتوری، یکی از راه‌های نمایش یک تابع سه بعدی در یک صفحه دو بعدی است. انگار از بالا به نمودار سه بعدی نگاه کرده و آن را در امتداد محور z فشرده می‌کنید. شکل 1b، که نسخه چرخانده شده شکل 1a است، مقداری شهود بصری برای شما فراهم می‌کند.
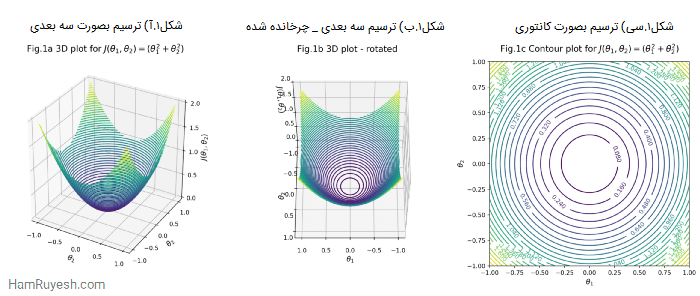
هنگام اعمال گرادیان کاهشی به این تابع، هدف ما همچنان ثابت می‌ماند، با این تفاوت که اکنون دو پارامتر برای بهینه سازی داریم (θ1 و θ2):
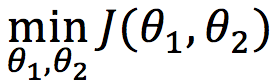
تا اینجا که همه چیز خیلی خوب بود!
قانون به روز رسانی (Update rule)
یکی دیگر از ویژگی‌های گرادیان کاهشی، این است که یک الگوریتم تکرار شونده (iterative) به شمار می‌آید. بنابراین، از قانون به روز رسانی برای به روز رسانی سیستمی و کارآمد مقادیر پارامترها پس از هر تکرار استفاده می‌کند.
هم رویش منتشر کرده است:
آموزش شبکه عصبی مصنوعی -- از صفر به زبان ساده
این قانون به‌روز رسانی برای گرادیان کاهشی تک متغیره به این صورت بود:
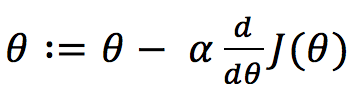
که در آن، α نرخ یادگیری (learning rate) است و dJ(θ)/dθ مشتق J(θ) است – یعنی شیب یک خط مماس بر J(θ) در نقطه θ.
اکنون که دو متغیر داریم، باید یک قانون به روز رسانی برای هر کدام ارائه کنیم:
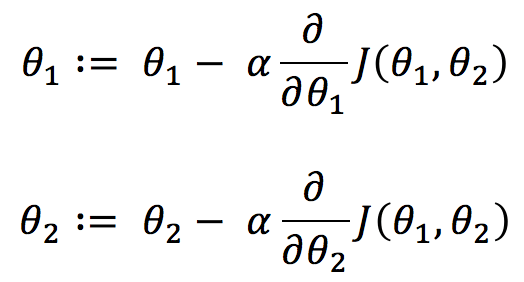
این معادلات تقریباً مشابه معادلات مربوط به توابع تک متغیره هستند. تنها تغییر در اینجا عبارت مشتق است، یعنی ∂J(θ1, θ2)/∂θ1 و ∂J(θ1, θ2)/∂θ2. اما نگران آن‌ها نباشید. نماد ∂ به جای d، به معنی مشتق جزئی (partial derivative) است.
+ پیش از این آموزش یادگیری ماشین در هم‌رویش منتشر شد. برای دیدن فیلم معرفی این آموزش بر روی این لینک (+) و یا پخش کننده پایین کلیک کنید:
برای دریافت بسته کامل این آموزش بر روی لینک زیر کلیک کنید:
آموزش یادگیری ماشین از صفر — یادگیری سریع و آسان
مشتق جزئی
در مشتقات جزئی، درست مانند مشتقات معمولی، ما همچنان به شیب خط مماسی علاقه مندیم که J(θ1, θ2) را در نقاط داده شده θ1 یا θ2 لمس می‌کند… اما این “یا” در اینجا بسیار مهم است.
اساساً، وقتی به خط مماس نگاه می‌کنیم، نمی‌توانیم θ1 و θ2 را همزمان حرکت دهیم. بنابراین، ما در هر زمان فقط بر روی یک متغیر تمرکز می‌کنیم، در حالی که متغیر دیگر را ثابت نگه می‌داریم. از این رو، نام آن را مشتق جزئی گذاشته‌ایم.
سعی خواهیم کرد این موضوع را با کمک یک نمودار بهتر توضیح دهم (به شکل 2 نگاه کنید). بیایید θ1 را به عنوان یک متغیر در نظر بگیریم و θ2 را ثابت نگه داریم، به عبارت دیگر، یک مشتق جزئی از θ1.
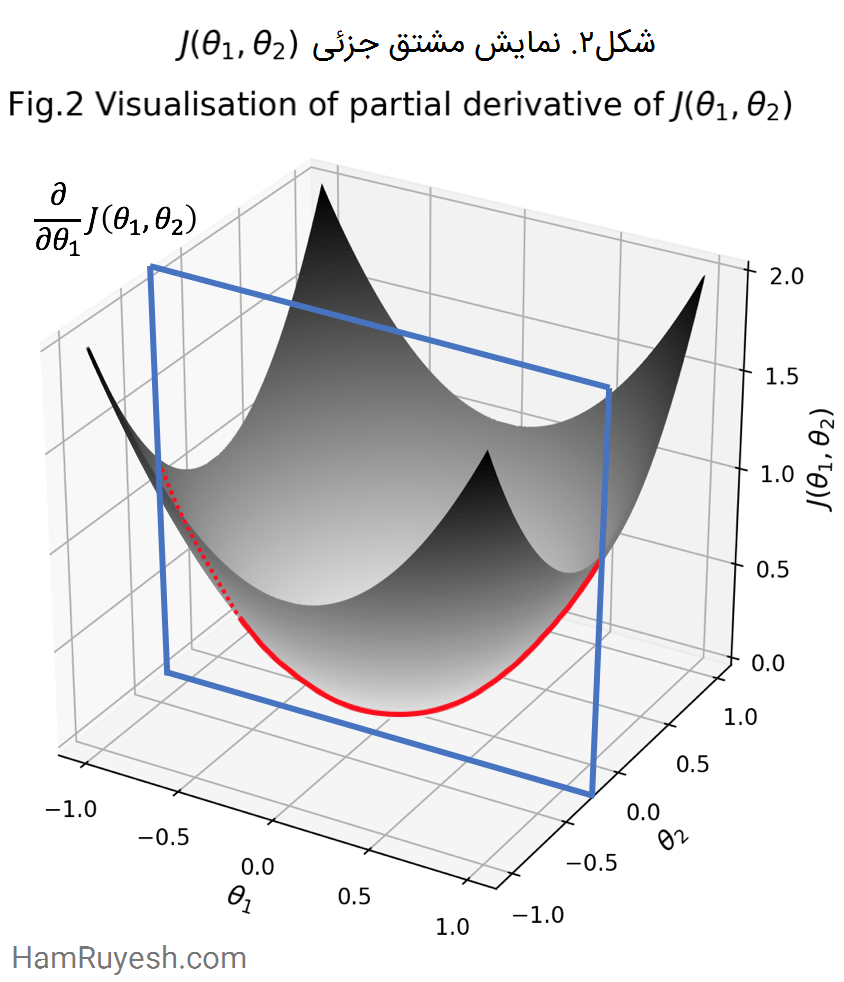
ثابت نگه داشتن θ2 از نظر بصری، به صورت یک صفحه θ1-J(θ1, θ2) (مربع آبی در شکل 2) است که نمودار را در یک مقدار خاص از θ2 برش می‌دهد. خط قرمز در شکل 2 نشان دهنده محل تقاطع بین صفحه θ1-J(θ1, θ2) و نمودار J(θ1, θ2) است که بیانگر تابع مورد نظر در مشتق جزئی است.
حال، اگر صفحه آبی را در راستای خط قرمز استخراج کنیم، در نهایت یک تابع تک متغیره خوب قدیمی با پارامتر θ1 در یک صفحه دوبعدی است، درست مانند آنچه در پست قبلی دیدیم!
هم رویش منتشر کرده است:
مشتق چیست و چه کاربردی دارد؟ -- مفهوم حسابان از صفر
بنابراین، می‌توانیم عبارت مشتق جزئی را در تابع به‌روزرسانی به صورت زیر محاسبه کنیم، زیرا ∂θ1 به سمت صفر می‌رود:
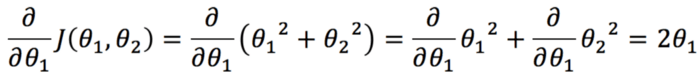
اثبات فرمول مشتق جزئی (اختیاری)
معادله بالا از یک فرمول شناخته شده برای مشتقات جزئی استفاده می‌کند، بنابراین اثبات نحوه محاسبه مشتق جزئی را برای رسیدن به 2θ1 حذف می‌کند. اگر علاقه‌ای به اثبات آن ندارید، لطفاً از این بخش صرفنظر کنید.
این قسمت برای شماست. اگر کمی شبیه من هستید و میل و وسواس زیادی برای دیدن آنچه در پشت صحنه اتفاق می‌افتد دارید!
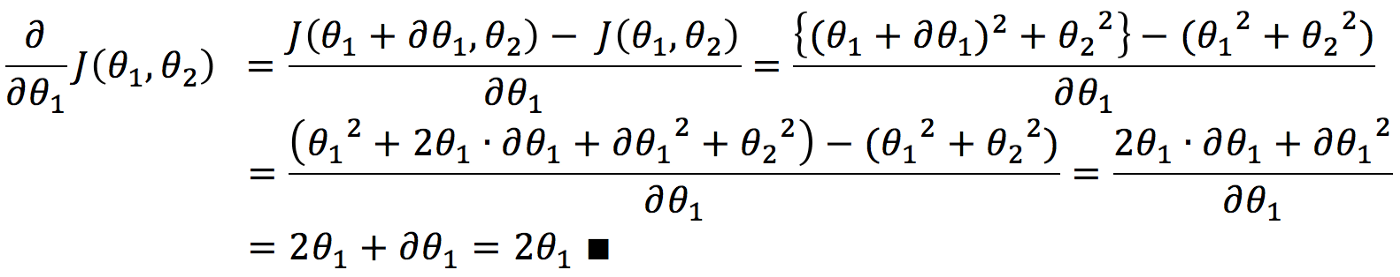
به روز رسانی همزمان
با اعمال یک منطق مشابه برای مشتق جزئی برای θ2، می‌توانیم قوانین به‌روزرسانی را به صورت زیر ساده کنیم:
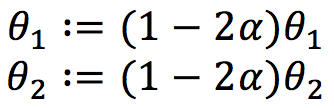
آخرین چیزی که باید به آن اشاره کرد، مفهوم به‌روز رسانی همزمان است. یعنی وقتی گرادیان کاهشی برای توابع چند متغیره اعمال می‌شود، به‌روزرسانی هر پارامتر باید در یک زمان اتفاق بیفتد، نه به صورت متوالی.
من یک توصیف شهودی برای شما پیدا کردم:
“راه رفتن، می‌تواند یک تشبیه شاده و خوب باشد. شما معمولاً ابتدا جهت شرق به غرب و سپس شمال به جنوب را طی نمی‌کنید. بلکه در کوتاه ترین جهت حرکت می‌کنید، یعنی در هر دو مختصات به طور همزمان حرکت می‌کنید.”
معنی آن در عمل این است که، در هر تکرار، باید هر یک از پارامترهای تازه محاسبه شده را به یک متغیر موقت اختصاص دهیم تا زمانی که محاسبه تمام پارامترها به پایان برسد. بنابراین ابتدا داریم:
سپس:
بسیار هم عالی! حالا ما همه تکه‌های پازل را برای ادامه کار در اختیار داریم.
درباره گرادیان کاهشی در عمل
لحظه موعود فرا رسید!
اکنون با استفاده از تابع J(θ1, θ2) = θ1² + θ2²، آماده هستیم تا گرادیان کاهشی چند متغیره را در عمل مشاهده کنیم. ما از نرخ یادگیری α = 0.2 و مقادیر اولیه θ1 = 0.75 و θ2 = 0.75 استفاده می‌کنیم.
شکل 3a نشان می‌دهد که گرادیان نزولی، چگونه به حداقل مقدار J(θ1, θ2) در نمودار کانتور نزدیک می‌شود. شکل 3b نمودار J(θ1, θ2) در ازای تعداد تکرارها است و برای مشاهده روند همگرایی استفاده می‌شود.
همانطور که در راهنمای سمت راست شکل می‌بینید، از تکرار هفتم تا هشتم، J(θ1, θ2) به مقدار 0.0056 کاهش می‌یابد که کمتر از حد آستانه 10^(-3) است، در این مرحله می‌توانیم همگرایی را اعلام کنیم.
بنابراین، ما ترکیبی از پارامترها را به صورت θ1 = 0.013 و θ2 = 0.013 پیدا کرده‌ایم که هدف ما را برآورده می‌کند.
جمع بندی
بسیار خوب، بنابراین این بار ما به کاربرد گرادیان کاهشی برای یک تابع چند متغیره نگاه کردیم. دفعه بعد، در ادامه به استفاده از گرادیان کاهشی در رگرسیون خطی خواهیم پرداخت. پس گوش به زنگ باشید!
کلیدواژگان
الگوریتم گرادیان کاهشی | الگوریتم گرادیان نزولی | گرادیان کاهشی | گرادیان کاهشی چیست | کاهش گرادیان | الگوریتم کاهش گرادیان | روش گرادیان کاهشی | درباره گرادیان کاهشی
منبع
machine-learning-bit-by-bit-multivariate-gradient-descent
دوره های آموزشی مرتبط
-
آموزش ساخت شبکه عصبی با پایتون (و دیگر زبان‌ها) از صفر
۱۳۲,۰۰۰ تومان -
آموزش بینایی کامپیوتر با پایتون و OpenCV ___ بسته جامع
۲۹۸,۰۰۰ تومان
